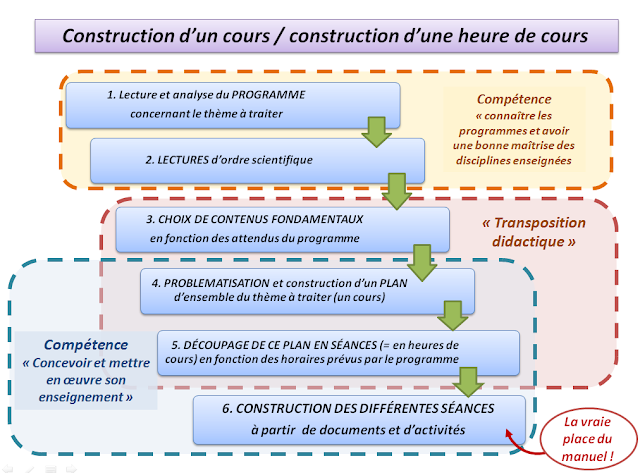
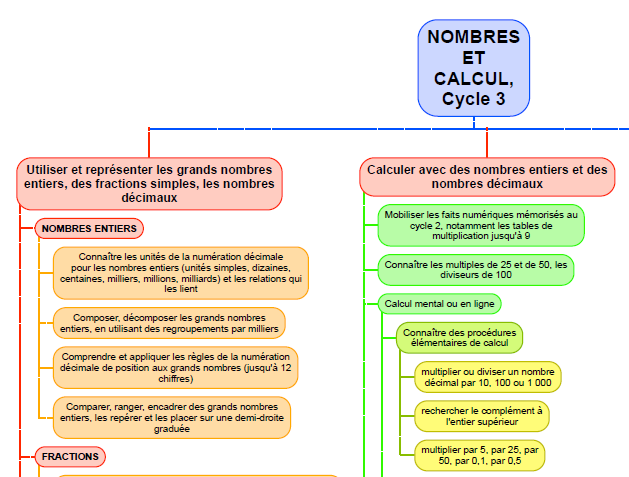
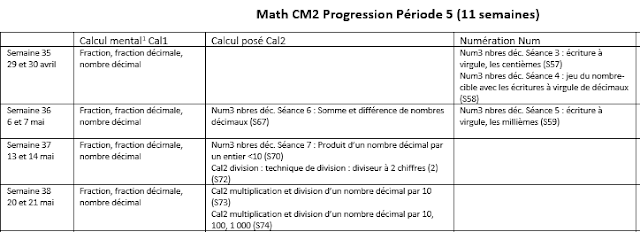
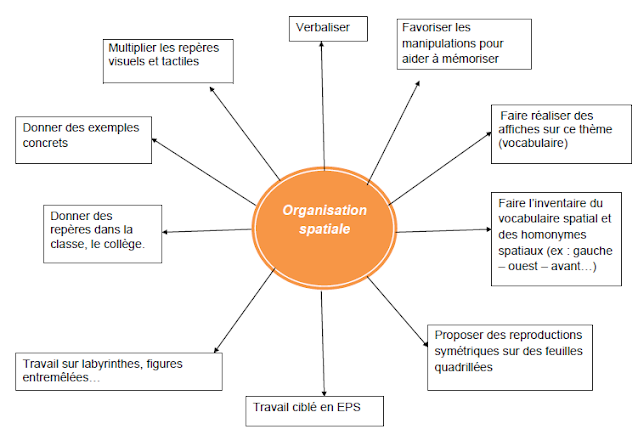
L'année dernière je n'ai proposé que peu de géométrie à mes élèves (rappel : des CM2 troubles dys associés +++, enfants hospitalisés de jour). Pour des raisons de temps (ils pouvaient avoir jusqu'à 2 heures de rééducation par jour sur le temps de classe - 1/2 jour débloquée, ils ont profité d'énormément de projets chronophages) et parce que je voulais tout reprendre avec eux. Mais différemment.
J'ai joué sur leur motivation: faire du beau dans leur cahier. Ainsi ils ont dessiné des frises géométriques, une par jour, en les coloriant, puis dans la dernière période des symétries (j'y reviendrai).
*
source: frises de CenicientaEt j'ai choisi, encore et toujours, de travailler avec eux les concepts en leur donnant du sens et en les manipulant.
Ce qui est compliqué avec des élèves dys sortis du circuit ordinaire (ceux que j'ai), c'est qu'ils ont, pour certains, tellement été cabossés par l'école ordinaire (je ne rentrerai pas ici dans les détails) ou qu'ils ont dû rentrer dans le moule, se faire transparents, qu'ils peuvent faire illusion, un peu. Par exemple, ils vont reconnaitre les formes planes à priori. Ils se font une image mentale du triangle. Mais dès que les formes géométriques sont sous une représentation non stéréotypée, il y a difficulté.


Voici des exemples de rectangles et de triangles non stéréotypés. Les formes sont penchées, tournées, les côtés ne sont pas verticaux, ni horizontaux. Nous n'avons pas le repère de la feuille pour nous aider: les côtés ne sont ni parallèles, ni perpendiculaires aux bords de la feuille. Le second rectangle propose des dimensions moins conventionnelles, le second triangle n'est pas particulier: il a 3 côtés de longueurs différentes et aucun angle droit. A chaque fois que je leur ai donné des formes géométriques, j'ai arrondi les bords de leur feuille pour qu'ils n'aient aucun côté droit.
***
Le vocabulaire géométrique doit avoir du sens, les propriétés sont explicitées. Nous avons repris les côtés, les sommets, les angles. Je me suis servi du fabuleux matériel suivant. Les côtés (barrettes rouges) et les sommets (flèches bleues) sont différenciés, indépendants. L'approche de l'angle droit s'est faite plus tard.
*source: Autisme et école inclusive
Et ils ont manipulé avec le non moins fabuleux matériel de l'atelier géométrique Montessori (oui, oui j'en ai un pour la classe, moi qui le rêvais pour le fiston).
Là, les sommets sont des épingles ou des attaches parisiennes, les côtés des barrettes de bois colorées.
***
En classe, je les fais rechercher avant de leur donner les informations et de mettre les affiches associées (ci-dessus).
(avec les barrettes Montessori)
- Pouvez-vous me construire un carré? (les élèves choisissent 4 barrettes colorées et forment un quadrilatère) Oh vous avez tous pris 4 barrettes, comment cela s'appelle en géométrie. (...) A. a pris 4 barrettes vertes, B. 2 barrettes vertes et 2 bleues, C. a pris 3 couleurs différentes. Lequel a construit un carré? (...) Qu'est-ce que cela veut dire quand les barrettes sont de même couleur?
- là pas encore de notion d'angle droit-
etc...
En individuel, L. a montré seule les différences entre carré et rectangle avant de les chercher sur le modèle de formes complexes associant des formes simples.
***
Mais alors, ils n'utilisent aucun instrument ? En fait, c'était assez rare car parmi mes élèves beaucoup avaient aussi une forme de dyspraxie. Difficile alors de tenir la règle, l’équerre, de mettre assez de pression avec une main sans bouger et de faire une trace précise sans trop appuyer, sans bouger, de l'autre.
Ils ont, paradoxalement, beaucoup tracer de cercles (réflexion approfondie grâce à une discussion de professeurs sur instag*). Oui oui, ce geste si délicat, peut-être encore plus complexe: le compas est le dernier instrument utilisé. Le geste de la main est travaillé autrement, la tenue et la pression des doigts (thamographe et spirographe), la rotation du poignet (la toupie).
La motivation du dessin et des couleurs.
***
Puis des ateliers. Le dessin à main levé en premier avec ce qu'il faut comme indices pour que je vois qu'ils ont compris (un carré peut ainsi être représenté comme un quadrilatère aplati si et seulement si les côtés ont été légendés comme de longueurs égales, un angle droit apposé; d'ailleurs je refusai les carrés plus ressemblant à priori mais sans légende, je prenais alors des barrettes et formais un quadrilatère autre que carré pour les pousser à me dire ce qui n'allait pas). (J'avais aussi pris beaucoup de temps avec le lutin de la maison à ce sujet ici.
Un tracé réel et une autocorrection grâce à du calque (fabuleux ateliers de Maitresse Margot, instag*)
***
Et j'ai travaillé avec eux le parallélisme, la perpendicularité, les angles, la symétrie. Je vous montrerai.